1-1 有効数字
PrimMath は基本的には IEEE754 による二進倍精度の計算を行っています。 有効数字は 15 桁、最大値は 1.7976931348623158×10308 、 0 以上の最小値は 2.2250738585072014×10-308(非正規化数除く)です。
1-2 0 と ∞
有限桁による計算であるため 0 の定義は正確な 0 ではなく、次の x が 0 と表されます。
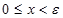 (1-1)
(1-1)
また、次の x が -0 と表されます。
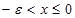 (1-2)
(1-2)
ここで、ε は計算の種類と扱う数値の大きさに依存する値です。 ε の最小値は 4.9406564584124654×10-324(非正規化数を含む最小値)になります。
∞ の定義は、次の x が ∞ と表されます。
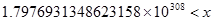 (1-3)
(1-3)
次の x が -∞ と表されます。
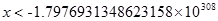 (1-4)
(1-4)
1-3 演算の優先順位
演算の優先順位は、出来るだけ見た目から普通に考えられる計算を実行するようにしてあります。
| 順位 | 演算 | 名前/意味 | 結合規則 |
|---|---|---|---|
| 1 | func[...] | []付関数 | - |
| :=func[...] | 代入関数 | → | |
| 2 | ! , !! | 階乗、二重階乗 | → |
| 3 | P,C | 順列、組合せ | → |
| 4 | 定数の前の省略乗算 | ← | |
| 5 | 定数の前以外での省略乗算 | ← | |
| func | 関数 | ← | |
| ^ | 累乗 | ← | |
| +, - | 単項プラス、単項マイナス | ← | |
| ~ | ビットNOT | ← | |
| ^ | 論理否定 | ← | |
| 6 | *, /, %, ×, ÷ | 乗算、除算、剰余 | → |
| 7 | +, - | 加算、減算 | → |
| 8 | >>, << | 右シフト、左シフト | → |
| 9 | & | ビットAND | → |
| 10 | |, ~ | ビットOR, ビットXOR | → |
| 11 | <, <=, >, >= | 小なり、以下、大なり、以上 | → |
| 12 | ==, != | 等価、不等価 | → |
| 13 | && | 論理積 | → |
| 14 | || | 論理和 | → |
| 15 | op= | 演算代入 | → |
| 16 | = | 代入 | ← |
順位4と順位5が独特と思いますが、これが自然な計算を実現しています。例を次に示します。
sin 2π ⇒ sin(2*π)(1-5)
-x^-a ⇒ -(x^(-a))(1-6)
1.2ι^2 ⇒ (1.2*ι)^2(1-7)
ιはPrimMath での虚数単位です。優先順位がもし心配ならカッコを付けることで解消されます。
特筆すべきは次の計算でしょう。
2 - -1^2 ⇒ 1(1-8)
2 - - 1^2 ⇒ 3(1-9)
式(1-8)では、’-‘と’1’の間に空白がないため、数値の’-1’の二乗を計算します。式(1-9)では、’-‘と’1’の間に空白があるため、’1’の二乗を計算して単項マイナスを計算し、2項演算の引き算を実行します。空白を識別するのは数値の場合だけであり、式(1-6)のように、変数の前の’-‘は空白があってもなくても単項マイナスです。
2-1 乱数
- 使用している関数
- rand
- 実数の一様乱数を生成して返す
- crand
- 複素数の一様乱数を生成して返す
- 使用しているコマンド
- なし
周期が 264 - 1 の Xorshift 法により、開区間 (0, 1) の二進倍精度の一様乱数を生成します。
極めて長い周期の乱数では初期値によっては偏った乱数列が一定期間続くことがあります。 もちろん、充分に長い乱数列で見れば良いのですが、使い方を誤ると問題を生じることがあります。 そのため、PrimMath では実用上ほとんど問題のない生成法を使用しています。
また、:setVarRand による乱数ジェネレータでは、周期が極めて長い メルセンヌツイスターも使用することができます。
3-1 フーリエ変換
- 使用している関数
- ::fourier
- ベクトルのフーリエ変換を実行したベクトルを返す
- ::invfourier
- ベクトルの逆フーリエ変換を実行したベクトルを返す
- 使用しているコマンド
- :draw2DGraphFourier
- グラフのフーリエ変更を実行してパワースペクトルのグラフを描画する
- :draw2DGraphCorr
- 2個のグラフの相関をとりグラフを描画する
離散フーリエ変換のデータ個数 N は、16 以上の 2 のべき乗になります。 入力の個数が 2 のべき乗でない場合は、 グラフのパワースペクトルではデータを中央に入れ下位と上位を 0 埋めします。 ベクトルの関数では下位にデータを入れて上位を 0 埋めします。
次に、フーリエ変換を使う上で必要となる一般的な説明をします。
フーリエ変換では、サンプリング周期を ts、フーリエ変換のデータ個数を N とすると、 周波数の分解能 Δf と最大の周波数 fmax は次式に従います。
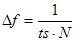 (3-1)
(3-1)
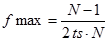 (3-2)
(3-2)
例えば、x 軸のレンジが 5 で、ポイント数が 1001 のグラフをフーリエ変換すると、 サンプリング周期 ts は 5/(1001-1)=0.005、データ個数 N は 1001 ですので、 周波数の分解能 Δf は 1/(0.005*1001) ≒ 0.1998、 最大の周波数 fmax は (1001-1)/(2*0.005*1001) ≒ 99.90 です。
フーリエ変換するときに単位は関係ありませんが、難しく考えるよりは、 普通に時間は sec、周波数は Hz とすれば悩むことはありません。
ここで、注意すべきは、式(3-1)よりサンプリング周期 ts を小さくすると周波数の分解能 Δf は大きくなる点です。
使う上でのポイントは次です。
(1)最大の周波数 fmax を大きくするには、サンプリング周期 ts を小さくする。
(2)周波数の分解能 Δf を小さくするには、データ個数 N を大きくする。
3-2 フィルタ
- 使用している関数
- なし
- 使用しているコマンド
- :draw2DGraphFilter
- グラフにフィルタを掛けてグラフを描画する
アルゴリズムは、ハニング窓を用いた直線位相となる FIR フィルタです。 そのため、急峻な振幅特性を得るためには次数を大きくする必要はありますが、 位相特性が直線位相でありグラフで見る感じは素直な特性と思います。
振幅が 10% から 90% に変化する幅 fw が大体次式で表されますので、 振幅特性の大まかな特徴を得ることができます。
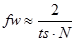 (3-3)
(3-3)
ここで、ts はサンプリング周期、N はフィルタの次数です。 設定するカットオフ周波数 fc では振幅が半分になります。 fc は次式を満たさなければいけません。
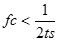 (3-4)
(3-4)
fc と fw を図で表したものが次です。
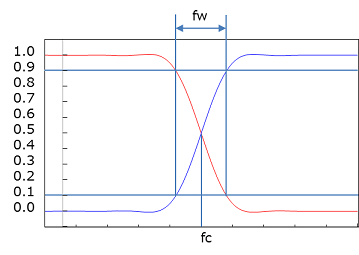
ここで、注意すべきは、式(3-3)よりサンプリング周期 ts を小さくすると fw は大きくなる点です。
使う上でのポイントは次です。
(1)振幅が 10% から 90% に変化する幅 fw を小さくするには、次数 N を大きくする。
4-1 回帰分析
- 使用している関数
- なし
- 使用しているコマンド
- :draw2DGraphDataFitFunc
- グラフを任意の式に当てはめて式のグラフを描画する
- :storeDataMultiRegres
- データ・ウィンドウのデータを重回帰分析して結果の予測値と残差をデータ・ウィンドウに格納する
非線形最小二乗問題として Marquardt 法を使用しています。 従ってパラメータが非線形の式にも適応します。
各パラメータの値は変数に代入され、標準誤差とパラメータの値との比を インフォメーションとして表示します。 この比はパラメータのばらつきに正規分布を仮定すればt検定の値として使用できます。 最小二乗問題ではパラメータが正規分布することを要求しませんが、 結果の評価を行うには正規分布を仮定します。
全体の各種評価値を t.Ans に格納します。
4-2 クラスタ分析
- 使用している関数
- なし
- 使用しているコマンド
- :storeDataCluster
- データ・ウィンドウのデータを分布に関係なく指定した個数に分類して結果をデータ・ウィンドウに格納する
- :storeDataNormDistrCluster
- データ・ウィンドウのデータを正規分布の混合として指定した個数に分類して結果をデータ・ウィンドウに格納する
EM アルゴリズムによる最尤法を用いています。このデータ解析は教師なし学習です。
正規分布を仮定できるのであれば正規分布の混合として分類したほうが良い結果が得られます。
4-3 クラス分類
- 使用している関数
- なし
- 使用しているコマンド
- :storeDataSVMLearn
- データ・ウィンドウのデータをSVMによる識別のために学習して結果をテーブル変数に代入する
- :storeDataSVMClassify
- データ・ウィンドウのデータをテーブル変数の値からSVMにより識別して結果をデータ・ウィンドウに格納する
ガウスカーネルを用いた 1-ノルムソフトマージン SVM の学習を行います。 このデータ解析は教師あり学習です。 マージンパラメータとガウスカーネルの標準偏差を設定することができます。 デフォルトでは、マージンパラメータに 100 を、 ガウスカーネルの標準偏差にはクラス間の平均距離を用います。 最初はデフォルト値で実行してみて、満足のいかない結果であれば パラメータを変更してみるとよいと思います。
学習の結果として、上限に達していないサポートベクトル数、 上限に達したサポートベクトル数、識別外れ値のサンプル数、 をインフォメーションとして表示します。
3 クラス以上の識別では、一対他方式を使用して決定関数が最大になるクラスに識別します。
5-1 微分・積分
- 使用している関数
- なし
- 使用しているコマンド
- :getValFuncDiff1
- 式と値を与えて1階微分した結果をAnsに代入する
- :getValFuncDiff2
- 式と値を与えて2階微分した結果をAnsに代入する
- :getValFuncDiffn
- 式と値を与えてn階微分した結果をAnsに代入する
- :getValFuncInte
- 式と値を与えて積分した結果をAnsに代入する
1 階微分は次の式で計算します。
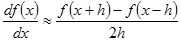 (5-1)
(5-1)
最適な h の値を求めるために繰返し処理を行っています。 最初は x の値の 1/1000 程度の値から始めて毎回半分にしていき、 前回との差分から誤差を推定して誤差が減少している限り繰返します。
2 階微分は同様に次の式で計算します。
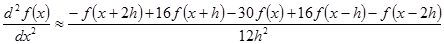 (5-2)
(5-2)
任意の n 階微分も同様に次の式で計算します。
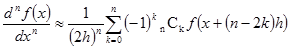 (5-3)
(5-3)
n が負数のときは、次式により積分します。
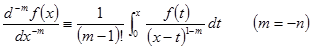 (5-4)
(5-4)
積分は、万能ではありませんが比較的広範囲に適用できる計算方法として、 Romberg 積分に中点則を用いています。 これは、端点に特異点があっても計算できます。 精度を上げるために積分区間を収束するまで分割して計算します。 計算は複素数で計算できますが、積分区間は実数で指定する必要があります。
積分区間が ∞ の場合には次式を用います。
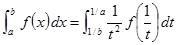 (5-5)
(5-5)
5-2 方程式の解
- 使用している関数
- なし
- 使用しているコマンド
- :getValSolveEq
- 方程式を与えて解く
連立方程式に対応した Newton 法を用いています。 1 変数の場合には、収束性を改善するために、減速という方法を使用しています。 初期値を虚数にすると複素数空間で解を求めます。
5-3 最適化問題
- 使用している関数
- なし
- 使用しているコマンド
- :getValMaximize
- 式を与えて最大となる変数の値を求める
- :getValMinimize
- 式を与えて最小となる変数の値を求める
アニーリング法を用いた滑降シンプレックス法を用いています。 不等式による制約条件を付加することができます。 グローバル・ミニマムを保証することはできませんが、 可能な限り探索するようになっています。 探索空間は実数です。
5-4 常微分方程式
- 使用している関数
- なし
- 使用しているコマンド
- :draw2DGraphOrdDiffEq
- 常微分方程式と初期値を与えて解をグラフに描画する
- :draw2DGraphSimulDiffEq
- 連立常微分方程式を解いてグラフに描画する
適応刻み幅制御を行う Runge-Kutta 法を用いています。 刻み幅は可変ですが、グラフを描画する際には 指定したポイント数に時間間隔が一定になるように出力します。
5-5 偏微分方程式
- 使用している関数
- なし
- 使用しているコマンド
- :storeDataPartDiffSta
- 2 次元ラプラス方程式を解いて結果をデータ・ウィンドウに格納する
- :storeDataPartDiffKinet
- 1 次元拡散方程式、1 次元波動方程式を解いて結果をデータ・ウィンドウに格納する
偏微分方程式を差分法により解きます。 差分法による万能な解法はないのですが、各方程式について比較的広範囲に 適用できると考えられる解法を採用しています。
2次元ラプラス方程式は次式で表されます。
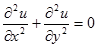 (5-6)
(5-6)
ラプラス方程式は初期条件を与えて SOR 法により解きます。
1次元拡散方程式は次式で表されます。
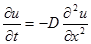 (5-7)
(5-7)
拡散方程式は Crank-Nicolson の陰解法により解きます。 初期値を x の関数として与え、端点の境界条件を値もしくは微分係数で t の関数として与えます。
1次元波動方程式は次式で表されます。
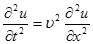 (5-8)
(5-8)
波動方程式は陽解法により解きます。 初期値を x の関数として与え、端点の境界条件を値もしくは微分係数で t の関数として与えます。
6-1 逆行列
- 使用している関数
- ::inv
- 行列を引数として逆行列を返す
- ::solve
- 行列とベクトルもしくは行列と行列を引数として連立1次方程式の解をベクトルもしくは行列として返す
- ::det
- 行列を引数として行列式を返す
- 使用しているコマンド
- なし
ピボット選択をした LU 分解を行っています。
6-2 特異値分解
- 使用している関数
- ::svd
- 行列を引数として特異値と特異ベクトルを返す
- ::pinv
- 行列を引数として疑似逆行列を返す
- ::leastsqr_solve
- 行列とベクトルもしくは行列と行列を引数として最小二乗解をベクトルもしくは行列として返す
- ::rank
- 行列を引数として行列の階数を返す
- 使用しているコマンド
- なし
アルゴリズムは QR 法を基本としています。
6-3 固有値
- 使用している関数
- ::eigen
- 行列を引数として全ての固有値と固有ベクトルを返す
- 使用しているコマンド
- なし
対称行列か非対称行列かを判定して、アルゴリズムを使い分けています。 対称行列であれば、Householder 法を用いています。 この方法は、固有ベクトルが互いに直交します。 非対称行列は QR 法を基本として用いています。